導磁率 (μ) 描述了材料與磁場的相互作用。為了分析導磁率可以用一個電感加電阻來進行類比，其中用電阻表示磁性材料中的磁芯損耗。如果在電感上并聯直流電流源，則磁芯材料中的電感與導磁率有關。

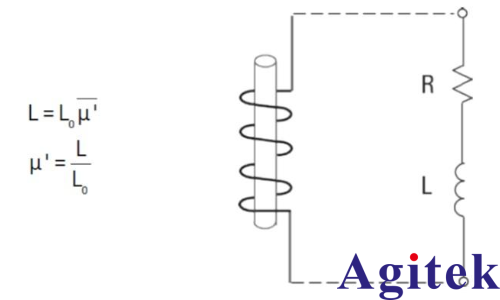
圖 . 電感器

在方程式中，L 是材料的電感，L 0 是線圈的自由空間電感，μ' 是實際導磁率。如果在同一電感器上并聯一個交流正弦電流源，得到的電壓將包含感應電壓和與導磁率有關的損耗電壓兩部分。磁芯損耗可以用與電感器 (L) 串聯的電阻 (R) 表示。復數導磁率 (μ* 或 μ) 由表示電能儲存項的實部 (μ') 和表示電能損耗項的虛部 (μ") 組成。相對介電常數 μr 是相對于自由空間的介電常數:

鐵 (鐵氧體)、鈷、鎳及其合金等材料具有較大的磁性；但許多材料沒有磁性，其導磁率與自由空間的導磁率 (μr = 1) 非常接近。另一方面，所有材料都具有介電特性，因此本文討論的重點主要是導磁率測量。

電磁波傳播

在時變條件下 (例如正弦波)，電場和磁場會同時出現。電磁波在自由空間中的傳播速度可以達到光速 c = 3 x 108 m/s，但在材料中的傳播速度慢得多。電磁波有不同的波長。信號波長 l 與頻率 f ( λ = c/f ) 成反比，因此隨著頻率的增加，波長會減小。例如在自由空間中，10 MHz 信號的波長為 30 m，而 10 GHz 信號的波長僅為 3 cm。電磁波的傳播在很多方面是由材料的介電常數和導磁率決定的。我們從 "光的角度" 來分析電介質特性。假設在自由空間中有一個材料平面板 (MUT)，一個 TEM 波入射到其表面 (圖 5)，從而產生入射波、反射波和發射波。由于材料中的波阻抗 Z 與自由空間阻抗 η (或 Z0) 不等 (更低)，因此會出現阻抗失配，產生反射波。一部分能量會滲透到樣品中。波一旦進入平板，

波速 v 就會變得比光速 c 慢。根據下面的方程式可知，波長 λd 比自由空間中的波長 λ0 更短。由于材料始終會產生某些損耗，波會出現衰減或插入損耗。為了方便計算，不考慮第二個邊界處的失配。

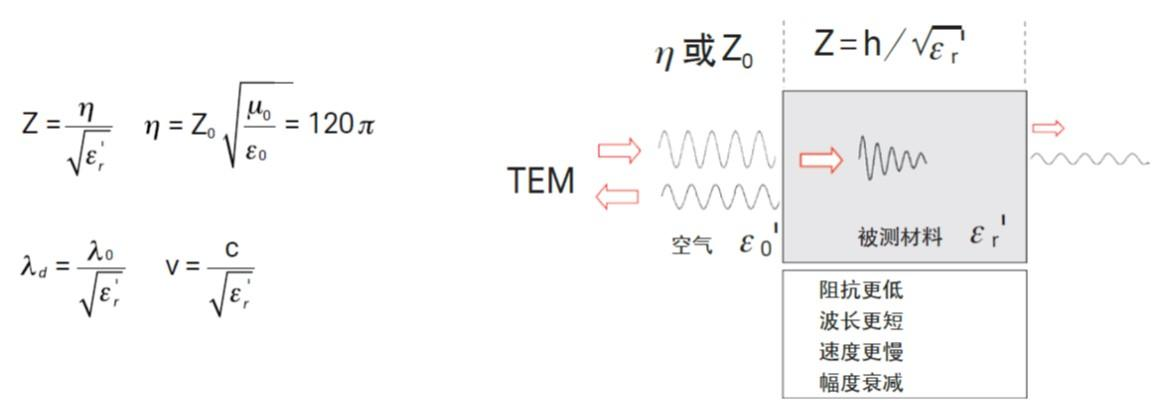
圖. 反射和發射信號

描述了在樣品無限長 (不考慮樣品背面的反射) 條件下，被測材料 (MUT) 介電常數與反射系數 | Γ?| 之間的關系。可以看出來，介電常數的值較小時 (20 以下)，較小的介電常數變化就會導致反射系數有很大的變化。在此范圍內用反射系數進行介電常數測量，靈敏度較高，因此精度也較高。相比之下，當介電常數的值較大時 (例如 70 至 90 之間)，反射系數隨介電常數的的變化極小，測量的不確定度就會比較大。

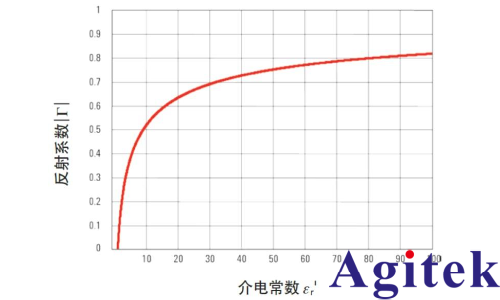
圖. 反射系數與介電常數的對比

介電機理

材料自身的多種介電機理或極化效應。介電材料中包含有序排列的電荷載流子，這些載流子如果受到電場作用，將會發生位移。極化導致電荷對電場進行補償，正電荷和負電荷會朝相反方向移動。

從微觀角度上看，有多種介電機理會對介電特性產生影響。偶極子取向和離子傳導在微波頻率上會發生強烈的相互作用。例如，水分子是永久性偶極子，在交替電場的作用下會發生旋轉。這些機理具有非常大的損耗 ― 這可以解釋為什么微波爐能夠加熱食物。原子和電子機理相對較弱，在微波范圍內通常是恒定不變的。每個介電機理都具有特征的 "截止頻率"。隨著頻率的增加，較慢的機理會依次退出，只剩下較快的機理，用 ε ' 表示。損耗因子 ( ε r" ) 將會在每個臨界頻率上達到相應的峰值。對于不同的材料，每個機理的幅度和 "截止頻率" 都是獨一無二的。水在低頻范圍內具有非常強的偶極子效應，但是其介電常數在 22 GHz 附近會明顯下降。另一方面，PTFE 沒有偶極子機理，其介電常數在毫米波范圍內也是非常恒定的。

諧振效應通常與電子或原子偏振有關。弛豫效應通常與取向偏振有關。

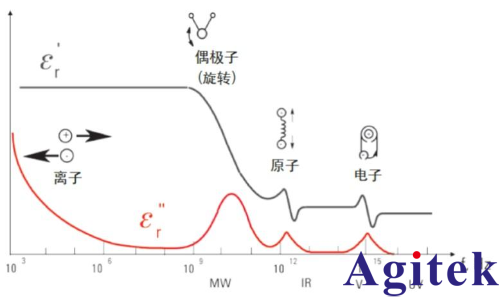
圖 . 介電機理的頻率響應

取向 (偶極子) 偏振

分子是由多個原子組成，這些原子會共享一個或多個電子。電子的重新排列可能導致電荷分布失衡，形成永久性偶極子矩。在沒有電場作用的條件下，這些力矩的方向是隨機的，不存在偏振。電場 E 將在電偶極子上施加扭矩 T，該偶極子將旋轉到與電場方向對齊，導致取向偏振發生。如果電場方向改變，扭矩也將隨之改變。

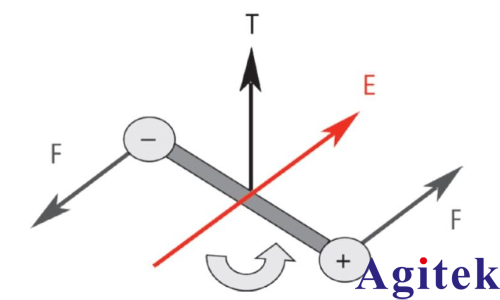
圖 . 電場中的偶極子旋轉

偶極子取向過程中產生的摩擦將會導致電介質損耗。偶極子旋轉會導致 ε r' 和 ε r" 同時在弛豫頻率上發生變化 (通常是在微波范圍內發生)。我們前面提到過，水是一種具有強烈取向偏振的物質。

電子和原子偏振

當電場推動原子核相對于周邊電子發生位移時，中性原子中會發生電子偏振。當相鄰的正離子和負離子在電場的作用下發生 "伸展" 時，會發生原子偏振。對于許多干性固體，盡管實際諧振是在更高頻率上發生，但是絕大部分偏振機理都處于微波頻率上。在紅外和可見光頻率范圍內，必須將電子沿軌道旋轉的慣性考慮在內。原子可以用振蕩器模型來描述，其具有類似于機械彈簧和質量系統的阻尼效應。在除諧振頻率之外的其他頻率上，振動幅度將非常小。電子和原子機理遠遠小于諧振，在 ε r' 中只占極小部分且恒定不變，幾乎是無損的。諧振頻率通過諧振響應 ε r' 和最大吸收峰值 ε r" 來識別。在諧振頻率以上，這些機理的作用將消失殆盡。

弛豫時間名詞解釋

弛豫時間 τ 衡量的是材料中的分子 (偶極子) 的移動性。位移的系統現在必須與電場方向對齊，以便返回隨機均衡值的 1/e (或偶極子現在必須在電場中取向)。液體和固體材料的分子處于凝聚態，即便在電場中也無法自由移動。恒定不變的碰撞將導致內部摩擦，因此分子將緩慢轉動并按照指數規律接近取向偏振的最終狀態，其弛豫時間常數為r 。當電場關閉后，這一順序將反轉，最終恢復隨機分布，時間常數相同。弛豫頻率 fc與弛豫時間成反比: 在弛豫頻率以下的頻率上，電場的交替速度將變慢，

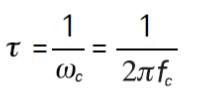
足以使偶極子能夠跟上電場的變化。由于偏振能夠完全形成，所以損耗 ( ε r" ) 與頻率直接成正比。隨著頻率的增加，ε r" 會連續增加，但是受偶極子對齊和電場之間相位滯后的影響，儲存電能 ( ε r' ) 開始減少。在弛豫頻率以上的頻率上，由于電場交替過快而無法影響偶極子的旋轉，取向偏振消失，ε r" 和 ε r' 將會同時下降。

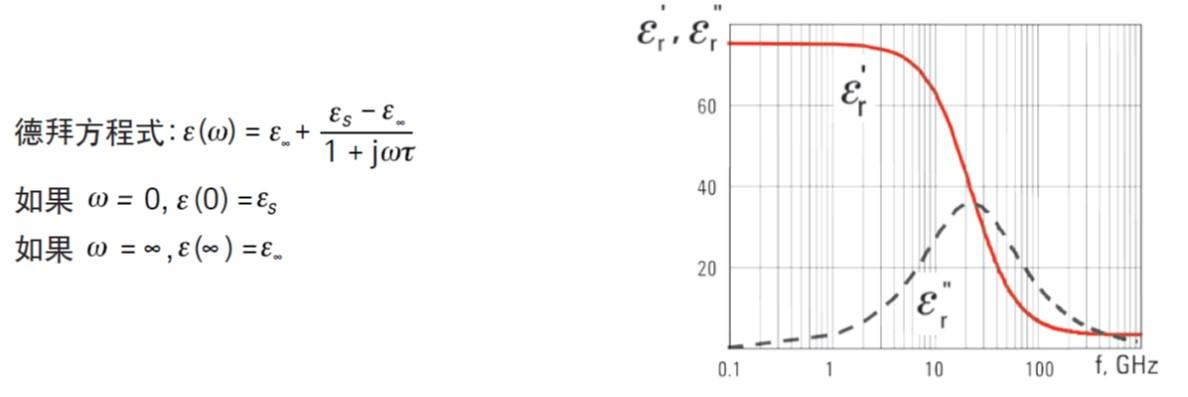
圖 . 水在 30 °C 時的徳拜弛豫

德拜關系式

具有單一弛豫時間常數的材料通過徳拜關系式進行建模，它由頻率決定，在介電常數中表現為特征響應。ε r' 是高于和低于弛豫的常數，在弛豫頻率 (22 GHz) 附近發生跳變。另外，ε r" 稍高于和低于弛豫，在弛豫頻率上的跳變區域中達到峰值。

在計算以上曲線時，介電常數的靜態 (直流) 值為 ε s = 76.47，介電常數的光 (無窮頻率) 值為 ε ∞ = 4.9，弛豫時間 τ = 7.2 ps。

科爾-科爾圖

復數介電常數還可以在科爾-科爾圖中顯示，縱軸表示虛部 ( ε r" )，橫軸表示實部( ε r' )，頻率作為獨立的參數。科爾-科爾圖在某種程度上類似于史密斯圓圖。具有徳拜關系式所表示的單一弛豫頻率的材料，將顯示為半圓，圓心位于 ε r" = 0 橫軸上，損耗因數峰值位于 1/τ。具有多個弛豫頻率的材料將顯示為半圓 (對稱分布) 或弧形 (不對稱分布)，其圓心位于 ε r" = 0 橫軸下方。

圖 中的曲線為半圓，圓心在 x 軸上，半徑為

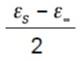
介電常數虛部最大值 ε 'rmax 等于半徑。頻率在曲線上沿逆時針移動。

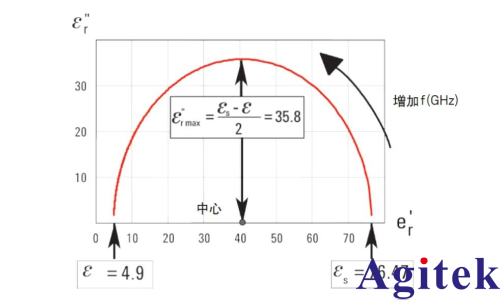
科爾-科爾圖

離子電導率

測得的材料損耗實際上可以表示為電介質損耗 ( ε rd")和電導率 (s) 的函數。

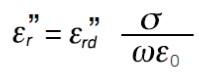
在低頻范圍內，總體電導率可能是由許多不同的傳導機理組成，但是在大多數材料中離子電導率是最普遍的。溶劑 (通常是水) 中的自由離子所產生的電解傳導對 ε r" 有極大影響。離子電導率只會增加材料中的損耗。在低頻范圍內，離子電導率的效應與頻率成反比，表現為 ε r" 曲線的 1/f 斜率。

界面或空間電荷偏振

當電荷在原子、分子、固體或液體的結構中受到區域限制，將發生電子、原子和取向偏振。材料中還含有電荷載流子，當施加低頻電場時，電荷載流子可以在材料中進行遷移。當這些電荷的遷移運動受到阻礙時，就會發生界面或空間電荷偏振。電荷可以在材料界面中被捕獲。當電荷不能在電極上自由放電或進行替換時，其運動也有可能受到阻礙。這些電荷的積聚導致的場失真會增加材料的總體電容，表現為 ε r' 的增加。

在低頻范圍內，材料混合物在彼此不接觸 (由非導電區隔離) 的導電區內會表現出麥克斯韋-瓦格納效應。如果電荷層非常薄且遠遠小于離子尺寸，那么電荷會獨立地與臨近粒子上的電荷發生響應。在低頻范圍內，電荷有時間在導電區的邊界上積聚，導致 ε r' 增加。但在高頻范圍內，電荷沒有時間進行積聚，由于電荷的位移與導電區的尺寸相比非常小，所以不會發生偏振。隨著頻率的增加，ε r' 會減小，損耗表現出與常規離子電導率相同的 1/f 斜率。

在這個低頻范圍內還可能發生許多其他介電機理，使介電常數發生明顯變化。例如，如果電荷層在厚度上接近或超過粒子尺寸，那么就會發生膠狀懸浮。此時，由于響應受到臨近粒子電荷分布的影響，所以麥克斯韋-瓦格納效應不再適用。

E4991B 阻抗分析儀