為了更高效地使用現有的有限帶寬資源，我們必須認識到，復合調制信號在時域中擴展，連續符號可能會重疊，這種情況被稱為碼間干擾 (ISI)。ISI 會導致接收機對信號的解讀 出錯。在頻域中，我們也同樣需要注意避免相鄰信道之間出現干擾。數據速率達到400 Gbps 和 1 Tbps 時，干擾問題將變得極其重要。

脈沖 Pulse

脈沖通常是指電子技術中經常運用的一種像脈搏似的短暫起伏的電沖擊(電壓或電流)。主要特性有波形，幅度，寬度和重復頻率。脈沖是相對于連續信號在整個信號周期內短時間發生的信號小大部分信號周期內沒有信號就像人的脈搏一樣。脈沖用于同步、觸發或控制測試中的多個測試設備。 脈沖還用于時鐘生成或雷達測試。 為了描述一個脈沖并使其創建可重復，定義了一組參數。 應用筆記

脈沖信號是什么意思?

在數字系統中，所有傳輸的信號都是通/斷的，即只有兩種電信號。這種電信號稱為脈沖信號，是所有數字系統中的基本電信號。現在一般指數字信號它已經是個周期內有一半時間有信號。計算機內的信號就是脈沖信號，又叫數字信號。

標準脈沖信號如下圖所示。

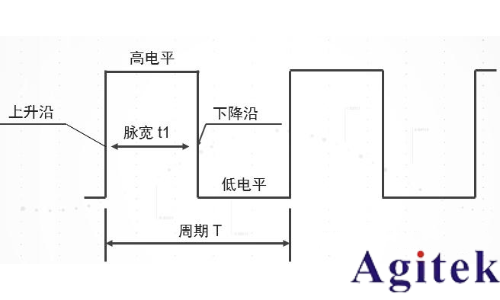
標準脈沖信號圖

脈沖信號基本特性

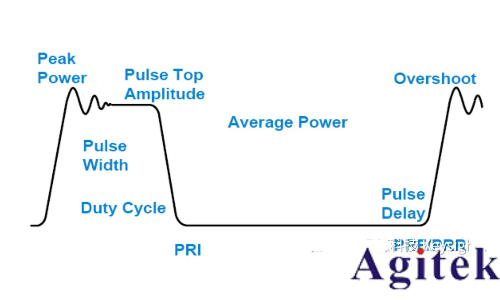
脈沖信號基本特性

脈沖信號最大的特性在于時域的不連續。時域的突發特性是脈沖用在雷達應用中的基本要求，因此脈沖信號參數也是雷達信號質量評估的主要指標。脈沖信號的時域不連續同時也給我們在功率及頻譜測試中增加了不少困難。

沖激信號

沖激，意思是持續時間極短，幾乎是瞬發的，同時作用也較為強烈，可以稱之為沖激。 激信號在數學上我們也叫沖激函數。

沖激信號 (Impulse signal)是指當時間t從負值趨于0時，它是一個強度為無限大的正的沖激函數，當時間t從正值趨于0時，它是一個強度為無限大的負的沖激函數。

沖激信號有三個特點：

1、除了時間t等于0之外幅值處處為零；

2、在時間t等于0處幅值為無窮大；

3、在包含沖激信號的位置上任意區間內面積為1。

脈沖信號和沖激信號區別

1.在特定點的取值不同

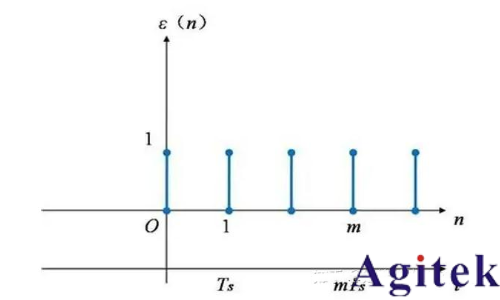
單位采樣序列δ(n)又稱為單位脈沖序列，其特點是在n=0時取值為1，其它取值為0。

單位沖激信號δ(t)在t=0時刻，取值無窮大。

2.在其他點的取值不同

單位采樣序列δ(n)在其它點取值都為0。

單位沖激信號δ(t)在整個區間內對時間t的積分為1，表示強度為1。

脈沖整形原理

脈沖整形是一種將輸入脈沖進行時域和頻域整形的技術。

在電子和電信領域，脈沖整形是改變傳輸脈沖的波形的過程。其目的是使傳輸的信號更適合其目的或通信渠道，通常是通過限制傳輸的有效帶寬。

通過這種方式過濾傳輸的脈沖，由信道引起的符號間干擾可以得到控制。在射頻通信中，脈沖整形是使信號適合其頻段的關鍵。通常，脈沖整形發生在線路編碼和調制之后。

脈沖整形的必要性

以高調制率通過頻帶有限的信道傳輸信號會產生符號間干擾。其原因是傅里葉對應關系（見傅里葉變換）。帶限信號對應的是一個無限的時間信號，它導致相鄰的脈沖重疊。隨著調制速率的增加，信號的帶寬也會增加。

只要信號的頻譜是一個尖銳的矩形，這就導致了時域中的sinc形狀。如果信號的帶寬大于信道帶寬就會發生這種情況，導致失真。這種失真通常表現為符號間干擾（ISI）。

從理論上講，對于正弦波形的脈沖，如果相鄰的脈沖完全對齊，即彼此處于零交叉點，就不會有ISI。但這需要一個非常好的同步和精確/穩定的采樣，沒有抖動。

作為確定ISI的一個實用工具，我們使用眼圖，它可以直觀地看到信道和同步/頻率穩定性的典型影響。信號的頻譜是由發射器使用的調制方案和數據速率決定的，但可以用脈沖整形濾波器來修改。

這種脈沖整形將使頻譜變得平滑，從而再次導致一個有時間限制的信號。通常情況下，傳輸的符號被表示為狄拉克-德爾塔脈沖乘以符號的時間序列。這就是從數字域到模擬域的正式過渡。在這一點上，信號的帶寬是無限的。然后用脈沖整形濾波器對這一理論信號進行濾波，產生傳輸信號。如果脈沖整形濾波器在時域上是一個矩形（就像在畫圖時通常這樣做），這將導致一個無限的頻譜。

在許多基帶通信系統中，脈沖整形濾波器隱含著一個盒式濾波器。它的傅里葉變換的形式是sin(x)/x，并且在高于符號率的頻率上有顯著的信號功率。

下面我們將介紹了消除干擾效應所需的各種條件，并描述了用于帶寬和信號隔離的不同濾波技術。

奈奎斯特 ISI準則

瑞典工程師 Harry Nyquist 在 20 世紀 20 年代曾經說過，為了消除 ISI，脈沖響應 h(t) 需要在時域中滿足以下要求：( H. Nyquist：《電報傳輸理論中的幾個主題》，Trans. AIEE，第 47 期，第 617-644 頁，1928 年 4 月)

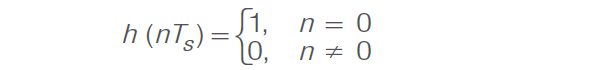
對于所有整數n ，TS 是相鄰脈沖的脈沖間隔。

圖 1 中使用了一個滿足 sinc (t) 脈沖條件的信號來闡述這一準則帶來的影響：脈沖重疊，但只有經過采樣的符號會對采樣時刻 tk 造成響應。其他的符號此時為零。通過這種方式，我們避免了 ISI 效應帶來的信號衰減和誤碼。

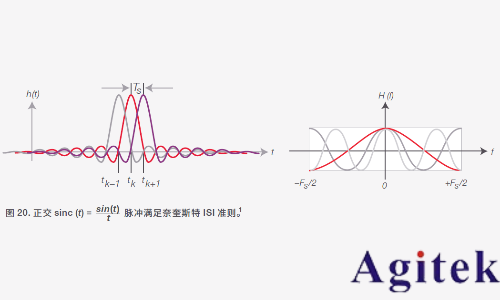
圖 1 右側顯示了脈沖響應的傅立葉變換 (FT)。可以看出，矩形頻率窗口內的頻率響應能夠滿足奈奎斯特 ISI 準則 ：

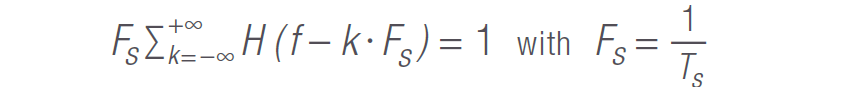
這意味著，諧波（頻率為奈奎斯特頻率 FS 整數倍的分量）必須加總為一個恒定值，以適應無 ISI 的頻段。奈奎斯特頻率 FS 是在不丟失信息的前提下對信號進行編碼所需的最小帶寬。

奈奎斯特脈沖整形

如上所述，sinc 信號非常適合用于預防 ISI，但它不實用，因為它會在時間上無限延長。為此，我們需要使用有限脈沖響應 (FIR) 濾波器在時域中截取這個信號。一個階數為 R 的 FIR 濾波器對應著 R+1 采樣點，隨后歸零。濾波器輸出 y[n] 的卷積僅考慮過去的采樣點 x[n-i]，因此可以實時進行過濾。

離散時間 FIR 濾波器的輸出 y[n] 與輸入 x[n] 有關系，如下所示 ：

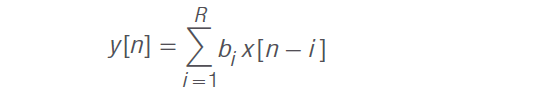
其中，bi 是濾波器系數。

為避免產生混疊，脈沖整形 FIR濾波器必須至少按 q = 2 的系數進行過采樣。換言之，在 TS 內必須至少有 1 個采樣點。由此，脈沖形狀可在接收機端重建，且不會丟失高頻分量。

圖 2 所示為以不同濾波器階數 R 濾波的 sinc 脈沖的濾波器結果，始終以 q = 2 的系數進行過采樣。功率譜是由正弦脈沖的矩形頻譜與矩形窗口的正弦形光譜的卷積產生。

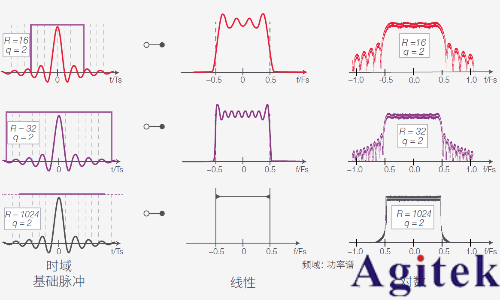
圖 2. 使用不同階數 R 的 FIR 濾波器截取 sinc 信號：在對采用線性和對數標度的功率譜進行快速傅立葉變換之后的時域波形

第一行中，濾波器階數為 16，信號跨越了 8 TS。在 FFT 中，可以看到有限時間窗口產生了失真。大部分功率位于奈奎斯特頻段 (-0.5 FS 至 0.5 FS），但有一部分位于頻段外。 功率譜以圖譜形式顯示諧波。

假設濾波器的長度增加一倍 (R = 32)，信號能夠更好地適應帶寬，但會出現振鈴。當 R = 1024 時，頻譜幾近完美；振鈴僅在陡峭邊沿上可見，功率譜還顯示出較少的帶外成分。遺憾的是，濾波器的階數 R 越高，濾波器設計的復雜程度也就越高。因此，通常希望采用滿足要求的最低階 R。

升余弦濾波器的概念

為了獲得更好的帶外抑制和無振鈴頻譜，升余弦濾波器是合適的備選方案。脈沖響應取決于滾降因數α（0 至 1 之間的任意值）：

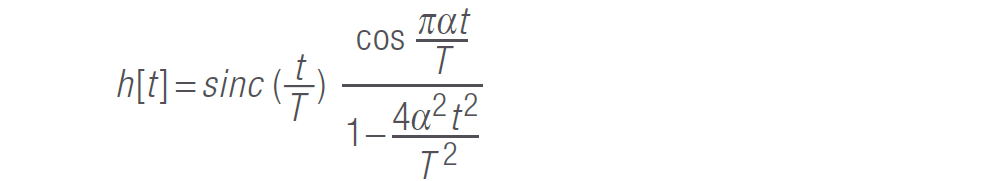
升余弦濾波器也能滿足奈奎斯特 ISI 準則，即，只有經采樣的符號會對信號造成響應。 在采樣點上的其他符號均為零。與 sinc 整形脈沖相比，升余弦信號要求更多的帶寬。

圖 3 描述了4 個不同滾降系數α 的濾波器響應：

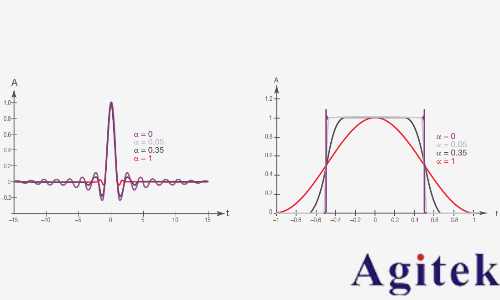
圖 3. 具有不同滾降系數的升余弦濾波器 ：歸一化時域和頻域呈現

在頻率響應中它表示，對于任何 α 值，曲線在 ±FS /2 的同一點上交叉，這是脈沖速率的一半。如前所述，這個是奈奎斯特頻率——在不丟失信息的前提下進行數據傳輸所需的最小帶寬。除此之外，當α = 1 時，幾乎沒有振鈴，但頻譜不會適應帶寬。

當α = 0 時，情況正好相反：頻率響應在帶寬范圍內為矩形（邊沿上的過沖僅僅是數學效應，也稱之為吉伯斯現象，沒有任何實際影響）。然而，時域信號顯示出更多振鈴。

在采樣點上，只有經過采樣的符號會對信號造成響應，但為什么振鈴會是問題？實際上， 當我們只在理想瞬間采樣時，其他的符號均為零，因此振鈴成為問題。在實際條件下，接收機幾乎不可能在這個點上進行精確采樣，因此在信號解讀時始終會有部分 ISI 產生誤差。

很明顯，時域中的帶寬限制和振鈴抑制之間需要進行權衡。對于每一個光纖應用，在選擇足夠的 α 值時都要加以權衡。

實際應用中的升余弦濾波器

我們仔細來看一下不同滾降系數對最有希望的 400 Gbps 調制方案的影響：16-QAM。 圖 4 顯示了頻域響應測量、眼圖測量、以及對星座點之間轉換產生的影響。

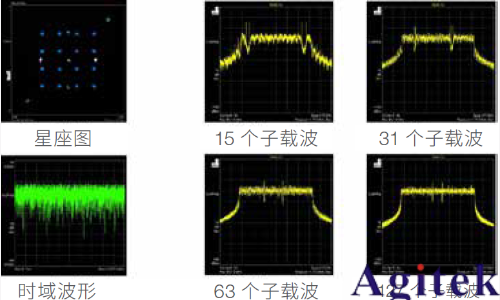
圖 4. 16-QAM 信號上的升余弦濾波器與滾降因數的關系 ：星座圖、眼圖和頻譜 ；使用 Keysight M8190A 任意波形發生器創建的信號。

上例顯示了無定形的矩形脈沖。已知只占據固定時間間隔的信號具有無限擴展的頻譜； 在頻率響應中可以看到大的旁瓣。眼圖顯示了開眼的寬帶信號的典型特性。在星座點之間存在直接轉換。

使用滾降系數α = 1 的升余弦濾波器，頻譜會變狹窄 ；不會再看到旁瓣。在眼圖中，眼圖張開度很大。星座點較小。這是帶寬較窄的系統的典型特征。接收機端的檢測帶寬也會降低，由此減少了噪聲。

當滾降系數α = 0.35 時，頻寬進一步減少，星座點的大小也隨之降低。星座點的轉換開始顯示很多過沖。這是因為當帶寬降低時，符號間的跳變時間就會延長，體現在星座圖中就是星座點之間存在很長的跳變曲線。眼圖閉合，采樣時間變得更加重要。

在α = 0.05 時可以得到幾近完美的矩形頻譜。星座點之間的跳變顯示了較大的過沖。完全 閉合的眼圖表明，采樣點必須經過精確調整，以免產生誤差。

能夠獲得怎樣的頻譜效率？

為了解脈沖整形濾波器帶來的頻譜效率提升，我們將其與應用正交頻分復用 (OFDM) 所產生的效應進行比較。圖 5 簡單描述了OFDM原理，與奈奎斯特制式類似。

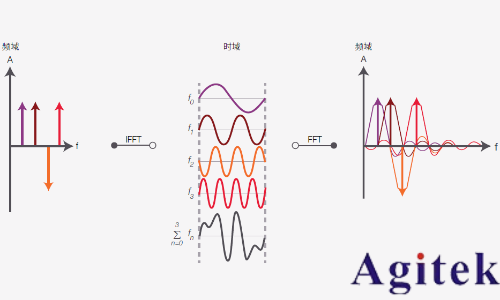
圖 5. 頻域和時域中的 OFDM

在 OFDM 中，頻率子頻譜是 sinc 形狀。為了提高頻譜效率，子頻譜會重疊，但由于它們存在正交性（以 π/2 的倍數位移），因此它們彼此間不會形成干擾。在時域中，符號是在固定的時間窗口中具有等距載頻 fn 的正弦曲線的總和。在本例中，單個信道的 4 個頻率上有 4 個子載波。在進行反向快速傅立葉變換 (IFFT) 之后，橘色跡線相移了π。

圖 6 顯示了對 16-QAM 調制 OFDM 信號進行頻譜分析。

圖 6. OFDM 對 16-QAM 信號頻譜的影響取決于子載波的數目；使用 Keysight M8190A 任意波形發生器 生成的信號

左上角是星座圖和時域波形。圖中有 15 個子載波和 2 個導頻，我們可以看到相對平坦的頻率頻譜和急劇的滾降。

通過增加子載波的數目，頻譜變得扁平，2 個導頻向中心移動。在基線上，可以看到頻譜隨著子載波數目的增加而趨向于矩形。

與奈奎斯特脈沖整形相比，它是如何提高頻譜效率的？

在圖 7 中，在奈奎斯特濾波器長度R（過采樣系數 q 選定為 2）上繪制了歸一化的頻譜效率 (SE)，與 OFDM 子載波數目 N 進行比較。

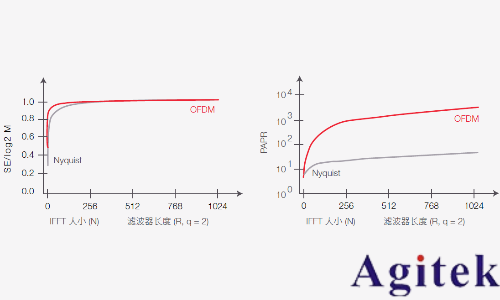
圖 7. 奈奎斯特脈沖整形與 OFDM 對頻譜效率和峰均功率比 (PAPR) 的影響

圖中顯示了兩種技術提供近似的頻譜效率。

歸一化峰均功率比 (PAPR) 的對比揭示了兩者在不同程度上具有類似的特性。OFDM 時域波形的 PAPR 更高。出現這種現象的原因是，在 OFDM 中，信號會呈現出高于平均功率值的一些峰值。由此，OFDM 電路和測試儀器需要較高的動態范圍，以避免因限制較高的功率電平而引起失真。